Clarifying: Axonometry, pt. 3

Taxonomy of Virtual Spaces

In part one of this series, I collated the qualities that define an axonometric projection.

An axonometric projection is one in which a rendered object can be measured across all three axes (x axis, y axis, and z axis).

The object's axes are not parallel and not orthogonal to the projection plane, allowing three faces of the object to be seen in the image.

It is a type of parallel projection in which a 3-D object is transformed into a 2-D image on the projection plane.

It is an affine transformation, meaning that the angles between lines in the image may differ from those found on the object, but straight lines remain straight and parallel lines remain parallel.

Being a parallel projection, lines do not converge and objects do not reduce in size with distance from the projection plane.

In part two of this series, I explored the histories of two different rendering styles that are both referred to as "axonometric" and both match the above description: oblique projection and isometric projection. Now, for a look at what a "projection" means in terms of rendering an image.

Planar Geometric Projections

fig. 1 from New Principles of Linear Perspective: Or the Art of Designing on a Plane, the Representations of All Sorts of Objects, in a More General and Simple Method Than Has Been Hitherto Done by Brook Taylor (1719)

Planar geometric projection is a geometric construct that seeks to define the abstract act of rendering a drawing of an object. In a planar geometric projection, points on a 3-D object are "projected" onto a 2-D projection plane. The geometry of the 3-D object is transformed in the process. How it is transformed depends on the projection method used to render the object on the plane.

There are three essential elements to this geometrical model (adapted from Drawing Distinctions by Patrick Maynard (2005) pg. 21):

1. One or more objects (usually straight-edged and cornered)
2. A planar surface on which the projection takes place
3. Projectors, straight lines that coordinate points between the other two elements

The illustration above shows a model of a perspectival projection (often known as linear perspective, a term coined by Brook Taylor in the 18th century (Maynard (2005) pg. 20). The object is a cube. Projector lines are projected from the corners of the cube, converging at the observer's eye (also called the station point, a stationary point from which the perspectival view is seen). The corners of the 2-D image of the cube are rendered at the points where the projectors intersect with the projection plane.

Figure 3-6a. Construction of an isometric projection from "Planar Geometric Projections and Viewing Transformations" by Ingrid Carlbom and Joseph Paciorek, Computing Surveys, vol. 10, no. 4 (1978) pg. 479

An isometric projection is a parallel projection where the projectors are all in parallel (not converging on a station point, or, imagining a station point at infinite distance) and are orthogonal (at 90 degrees) to the projection plane. None of the axes are in parallel with the projection plane, allowing three sides of the object to be rendered.

Figure 3-11a. Construction of an oblique projection from "Planar Geometric Projections and Viewing Transformations" by Carlbom and Paciorek (1978) pg. 482

An oblique projection is a parallel projection where the projectors are all in parallel and are at an oblique angle to the projection plane (often at 45 degrees). Two axes are parallel to the projection plane but, due to the oblique angle of the projectors, three sides of the object are rendered.

Primary Geometry and Secondary Geometry

The geometric projection model described above is what Peter Jeffrey Booker distinguishes as "Primary Geometry." This is the 3-D geometry of the lines of projectors from the scene to the eye of the viewer and the intersections of those projectors with a projection plane in order to form an image. He also notes "Secondary Geometry" as the 2-D geometry of the projection plane, itself (from A History of Engineering Drawing (1963))

Booker decried the primary geometry method as having "little practical significance or psychological reality" (as summarized in Art and Representation by John Willats (1997) pg. 38). 

"The modern method, described above, of defining the various drawing systems in terms of three-dimensional projective geometry was invented during the nineteenth century by textbook writers who wanted to give engineering drawing an air of authority by bringing it into line with Renaissance accounts of linear perspective. The idea of orthogonal projection as a variety of perspective with the object moved to an infinite distance away is a mathematical fiction, and engineers rarely, if ever, think of the system that way." Willats (1997) pg. 38

Fig. 2.1 Classification scheme for the projection systems, based on primary geometry. Adapted from British Standard 1192 (1969) from Willats (1997) pg. 39

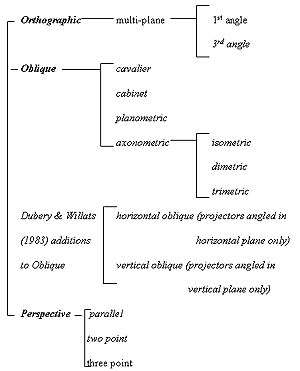
Willats (still arguing on Booker's behalf) also purports that "defining the various projection systems in terms of their primary geometry leads to a classification scheme which seems counter-intuitive" ((1997) pg. 39). He presents the British Standard 1192 of drawing classifications for technical drawings as such a system. Isometric (and related methods) are classed as a parallel projection with orthogonal methods, based on the fact that their projectors are orthogonal to the projection plane. Oblique (and axonometric, as defined in architecture) methods are in a separate parallel projection class based on the fact that their projectors are oblique to the projection plane.

Willat's classification scheme for projection systems based on secondary geometry (as adapted in Drawing as Transformation: From Primary Geometry to Sedondary Geometry by Howard Riley (2001))

Willats instead proposes a new system based on secondary geometry, focusing on the picture surface instead of an abstract system of projection. Here, orthographic refers only to rendered objects that face in parallel to the picture plane. Oblique and isometric are grouped together as methods that render three sides of an object that is at an oblique angle to the picture plane (note that Willats includes a few new oblique definitions first described in Perspective and Other Drawing Systems by Fred Dubery and John Willats (1983) pp 21-28).

Conclusion, and What's Right for Me

Willats rightly cites the primary geometry system of projection as unintuitive and not really how people think about drawing images.

However, my study is in computer graphics and there are a lot of cases where this method is how the computer makes a 2-D image from 3-D data. Graphics shaders make calculations both in eye-space (coordinates on the screen, akin to secondary geometry) and scene-space (coordinates in the virtual world, akin to primary geometry). The digital tools I wish to use in order to affect camera perspective in my digital project also function in a similar manner.

Figure 3-1. Classification of projections from "Planar Geometric Projections and Viewing Transformations" by Carlbom and Paciorek (1978) pg. 475

Insted, the taxonomic system I use is heavily based on the classification system found in "Planar Geometric Projections and Viewing Transformations" by Ingrid Carlbom and Joseph Paciorek, Computing Surveys, vol. 10, no. 4 (1978). This system has been an established standard in computer graphics for decades, and was incorporated (and slightly expanded upon) into Computer Graphics: Principles and Practice, Second Edition by Foley, van Dam, Feiner, and Hughes (1990) pg. 237. This system also matches the one adapted by the University of Montreal academics in their studies of digital game graphics (see "A New Angle on Parallel Languages" by Audrey Larochelle, GAME: The Italian Journal of Game Studies, vol. 1, no. 2 (2013) and "The Game FAVR: A Framework for the Analysis of Visual Representation in Video Games" by Dominic Arsenault, Pierre-Marc Côté, and Audrey Larochelle, Loading…Journal of the Canadian Game Studies Association, vol.9, no.14).

In this classification system, "axonometric" refers to isometric projection and its kin (dimetric and trimetric). Oblique is a separate classification based on the obliqueness of their projectors.

More on my taxonomy system in another blog post...